《勾股定理的应用》勾股定理PPT课件下载

人教版八年级数学下册《勾股定理的应用》勾股定理PPT课件下载，共22页。

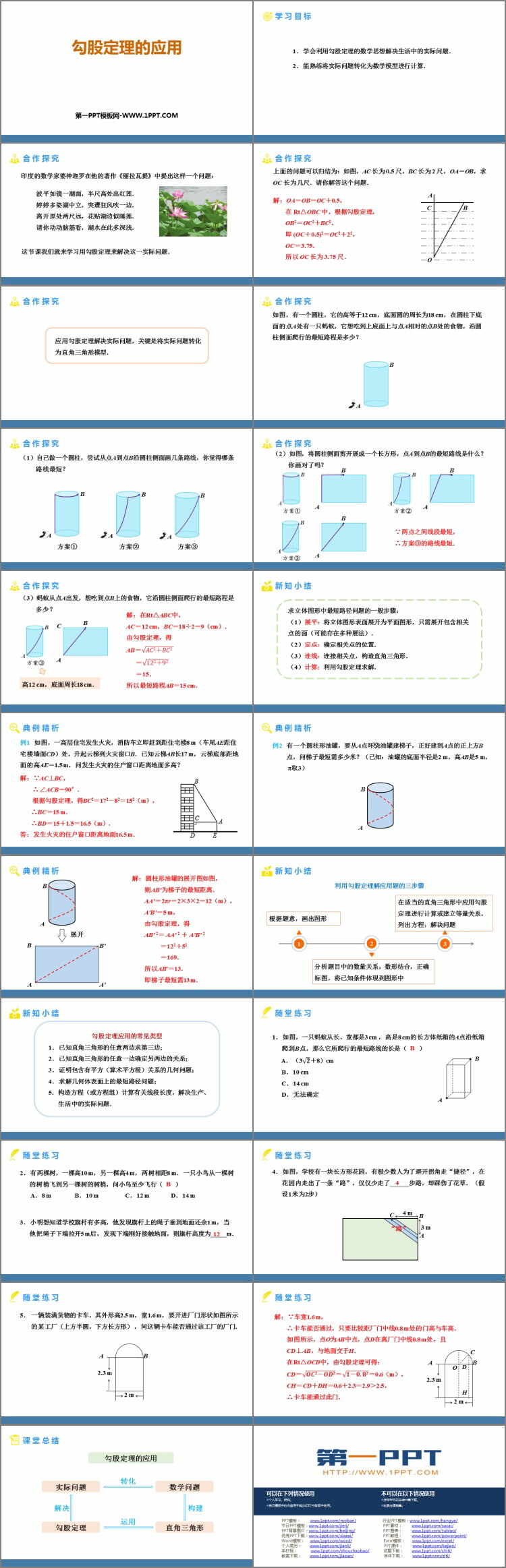
学习目标

1．学会利用勾股定理的数学思想解决生活中的实际问题．

2．能熟练将实际问题转化为数学模型进行计算．

合作探究

上面的问题可以归结为：如图，AC 长为 0.5 尺，BC 长为 2 尺，OA＝OB，求 OC 长为几尺．请你解答这个问题．

解：OA＝OB＝OC＋0.5，

在 Rt△OBC 中，根据勾股定理，

OB2＝OC2＋BC2，

即 (OC＋0.5)2＝OC2＋22，

OC＝3.75．

所以 OC 长为 3.75 尺．

应用勾股定理解决实际问题，关键是将实际问题转化为直角三角形模型．

如图，有一个圆柱，它的高等于12 cm，底面圆的周长为18 cm，在圆柱下底面的点A处有一只蚂蚁，它想吃到上底面上与点A相对的点B处的食物，沿圆柱侧面爬行的最短路程是多少？

（1）自己做一个圆柱，尝试从点A到点B沿圆柱侧面画几条路线，你觉得哪条路线最短？

（2）如图，将圆柱侧面剪开展成一个长方形，点A到点B的最短路线是什么？你画对了吗？

（3）蚂蚁从点A出发，想吃到点B上的食物，它沿圆柱侧面爬行的最短路程是多少？

求立体图形中最短路径问题的一般步骤：

（1）展平：将立体图形表面展开为平面图形，只需展开包含相关点的面（可能存在多种展法）．

（2）定点：确定相关点的位置．

（3）连线：连接相关点，构造直角三角形．

（4）计算：利用勾股定理求解．

典例精析

例1 如图，一高层住宅发生火灾，消防车立即赶到距住宅楼8 m（车尾AE距住宅楼墙面CD）处，升起云梯到火灾窗口B．已知云梯AB长17 m，云梯底部距地面的高AE＝1.5 m，问发生火灾的住户窗口距离地面多高？

解：∵AC⊥BC，

∴∠ACB＝90°.

根据勾股定理，得BC2＝172－82＝152（m），

∴BC＝15 m．

∴BD＝15＋1.5＝16.5（m）.

答：发生火灾的住户窗口距离地面16.5 m．