《两条直线的位置关系》相交线与平行线PPT免费课件(第1课时)

北师大版七年级数学下册《两条直线的位置关系》相交线与平行线PPT免费课件(第1课时)，共22页。

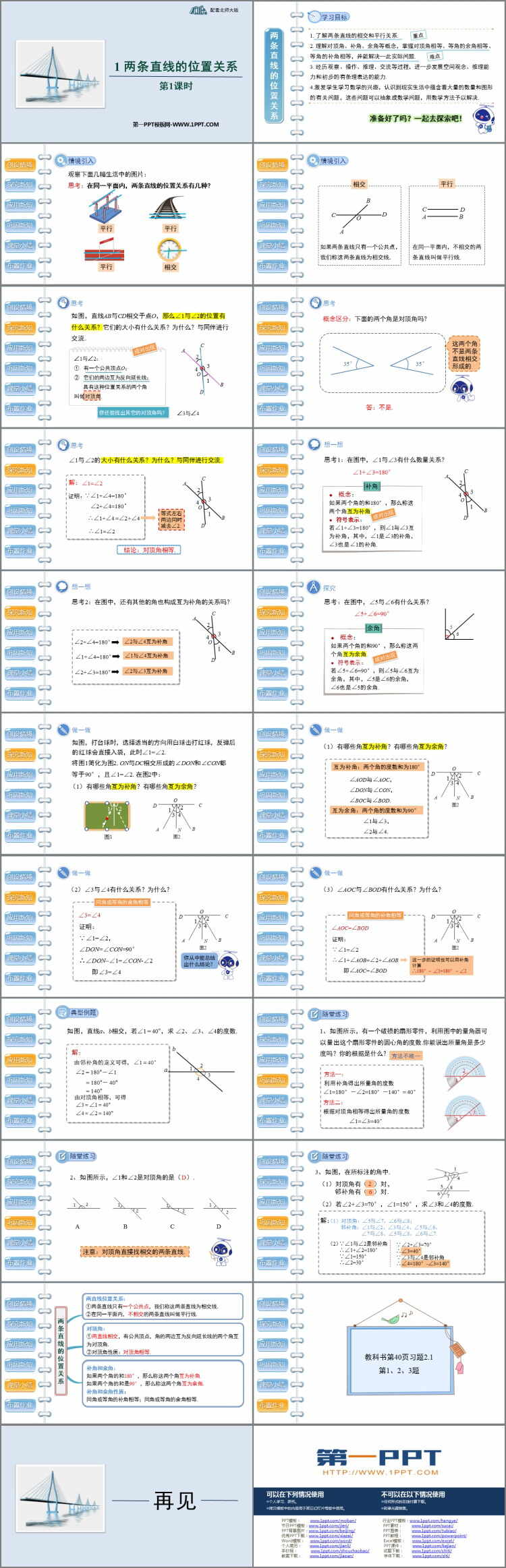
学习目标

1. 了解两条直线的相交和平行关系.

2. 理解对顶角、补角、余角等概念，掌握对顶角相等、等角的余角相等、等角的补角相等，并能解决一此实际问题.

3. 经历观察、操作、推理、交流等过程，进一步发展空间观念、推理能力和初步的有条理表达的能力.

4.激发学生学习数学的兴趣，认识到现实生活中蕴含着大量的数量和图形的有关问题，这些问题可以抽象成数学问题，用数学方法予以解决.

情境引入

如果两条直线只有一个公共点，我们称这两条直线为相交线.

在同一平面内，不相交的两条直线叫做平行线.

思考

如图，直线AB与CD相交于点O，那么∠1与∠2的位置有什么关系？它们的大小有什么关系？为什么？与同伴进行交流.

∠1与∠2：

有一个公共顶点O；

它们的两边互为反向延长线；

具有这种位置关系的两个角叫做对顶角.

概念区分：下面的两个角是对顶角吗？

这两个角不是两条直线相交形成的.

想一想

思考1：在图中，∠1与∠3有什么数量关系？

∠1+∠3=180°

概念：

如果两个角的和180°，那么称这两个角互为补角.

符号表示：

若∠1+∠3=180°，则∠1与∠3互为补角，其中，∠1是∠3的补角，∠3也是∠1的补角.

思考2：在图中，还有其他的角也构成互为补角的关系吗？

∠2+∠4=180° ∠2与∠4互为补角

∠1+∠4=180° ∠1与∠4互为补角

∠2+∠3=180° ∠2与∠3互为补角

思考：在图中，∠5与∠6有什么关系？

∠5+∠6=90°

概念：

如果两个角的和90°，那么称这两个角互为余角.

符号表示：

若∠5+∠6=90°，则∠5与∠6互为余角，其中，∠5是∠6的余角，∠6也是∠5的余角.

做一做

（1）有哪些角互为补角？有哪些角互为余角？

互为补角：两个角的度数和为180°

∠AOD与∠AOC，

∠DON与∠CON，

∠BOC与∠BOD.

互为余角：两个角的度数和为90°

∠1与∠3，∠2与∠4.

两直线位置关系：

①两条直线只有一个公共点，我们称这两条直线为相交线.

②在同一平面内，不相交的两条直线叫做平行线.

对顶角：

①两直线相交，有公共顶点，角的两边互为反向延长线的两个角互为对顶角.

②对顶角性质：对顶角相等.

补角和余角：

如果两个角的和180°，那么称这两个角互为补角.

如果两个角的和是90°，那么称这两个角互为余角.

补角和余角性质：

同角或等角的补角相等；同角或等角的余角相等.