《一次函数的应用》一次函数PPT精品课件(第1课时)

北师大版八年级数学上册《一次函数的应用》一次函数PPT精品课件(第1课时)，共20页。

复习旧知

1. 如何解答实际情景函数图像的信息？

（1）理解横、纵坐标分别表示的实际意义

（2）分析已知（看已知的是自变量还是因变量），通过做x轴或y轴的垂线，在图像上找到对应的点，由点的横坐标或者纵坐标读出要求的值

（3）紧扣实际意义去解释点的坐标

2. 解答实际情景函数图象信息问题的方法有哪些？

法一：函数图象观察法

法二：关系式计算法

情境引入

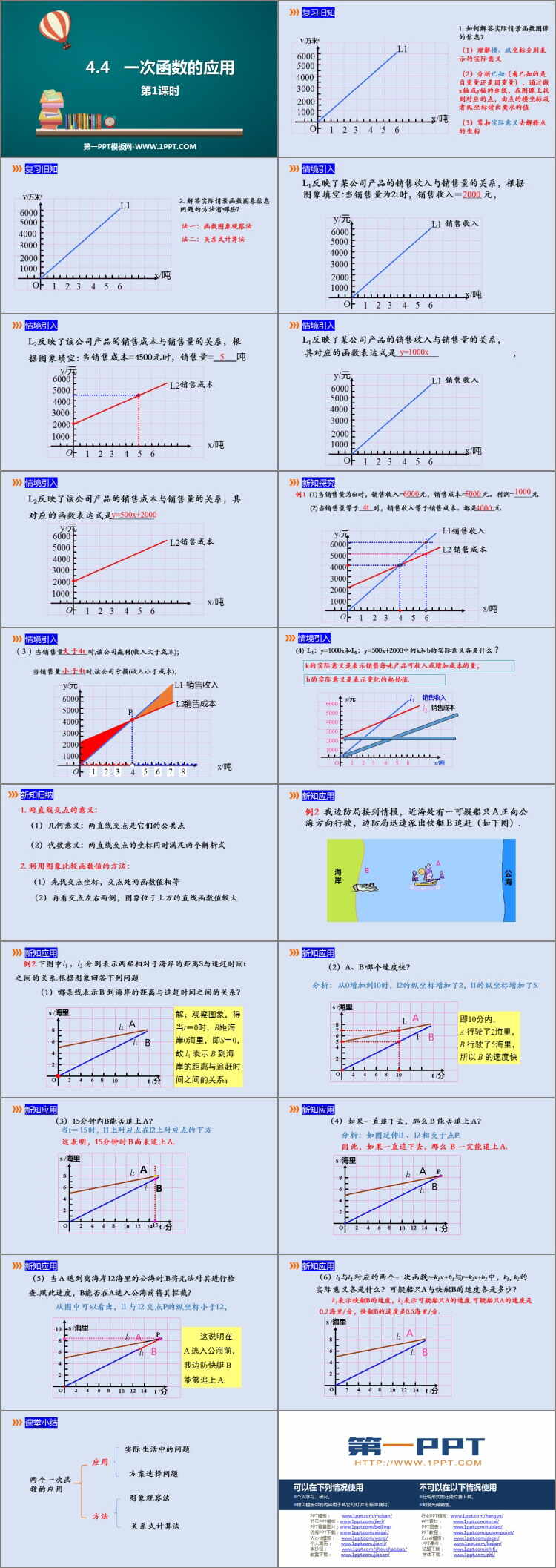
L1反映了某公司产品的销售收入与销售量的关系，根据图象填空：当销售量为2t时，销售收入＝____ 元，

L2反映了该公司产品的销售成本与销售量的关系，根据图象填空：当销售成本=4500元时，销售量=_____吨 　

新知归纳

1. 两直线交点的意义：

（1）几何意义：两直线交点是它们的公共点

（2）代数意义：两直线交点的坐标同时满足两个解析式

2. 利用图象比较函数值的方法：

（1）先找交点坐标，交点处两函数值相等

（2）再看交点左右两侧，图象位于上方的直线函数值较大

新知应用

例2.下图中 l1 ，l2 分别表示两船相对于海岸的距离S与追赶时间t之间的关系.根据图象回答下列问题

（1）哪条线表示 B 到海岸的距离与追赶时间之间的关系？

解：观察图象，得当t＝0时，B距海岸0海里，即S＝0，

故 l1 表示 B 到海岸的距离与追赶时间之间的关系；

（2）A、B 哪个速度快？

分析：从0增加到10时，l2的纵坐标增加了2，l1的纵坐标增加了5.

即10分内，A 行驶了2海里，B 行驶了5海里，所以 B 的速度快

（3）15分钟内B能否追上 A？

当t＝15时，l1上对应点在l2上对应点的下方

（4）如果一直追下去，那么 B 能否追上 A？

分析：如图延伸l1 、l2 相交于点P.

因此，如果一直追下去，那么 B 一定能追上 A.