《等腰三角形》三角形的证明PPT下载(第3课时)

北师大版八年级数学下册《等腰三角形》三角形的证明PPT下载(第3课时)，共22页。

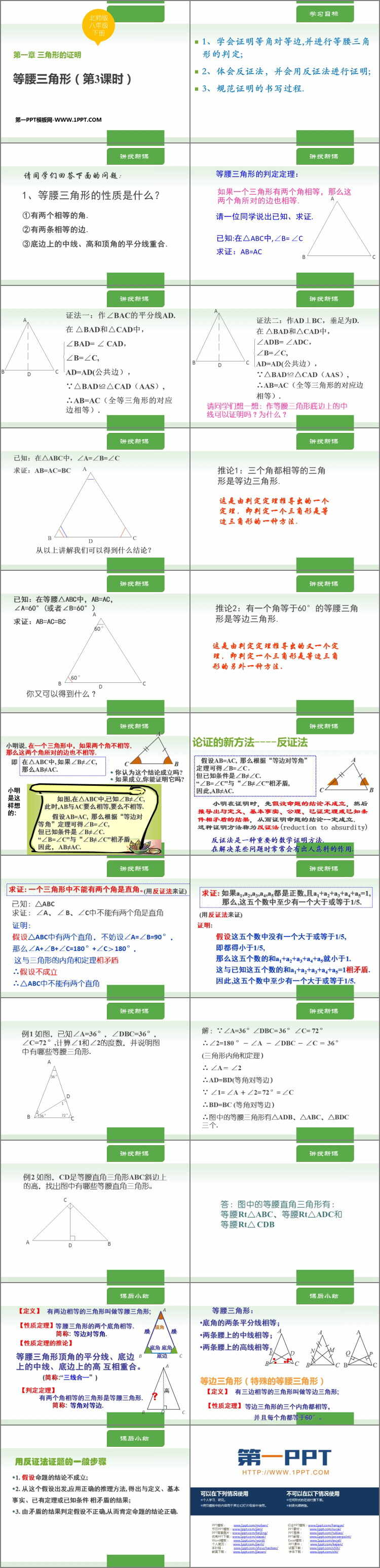
学习目标

1、学会证明等角对等边,并进行等腰三角形的判定;

2、体会反证法，并会用反证法进行证明;

3、规范证明的书写过程.

讲授新课

1、等腰三角形的性质是什么？

①有两个相等的角.

②有两条相等的边.

③底边上的中线、高和顶角的平分线重合.

等腰三角形的判定定理：

如果一个三角形有两个角相等，那么这两个角所对的边也相等.

已知:在△ABC中,∠B= ∠C

求证：AB=AC

证法一：作∠BAC的平分线AD.

在 △BAD和△CAD中，

∠BAD= ∠ CAD，

∠B=∠C,

AD=AD(公共边），

∵△BAD≌△CAD（AAS）,

∴AB=AC（全等三角形的对应边相等）.

证法二：作AD⊥BC，垂足为D.

在 △BAD和△CAD中，

∠ADB= ∠ADC，

∠B=∠C,

AD=AD(公共边），

∵△BAD≌△CAD（AAS）,

∴AB=AC（全等三角形的对应边相等）.

推论1：三个角都相等的三角形是等边三角形.

这是由判定定理推导出的一个定理，即判定一个三角形是等边三角形的一种方法.

推论2：有一个角等于60°的等腰三角形是等边三角形.

这是由判定定理推导出的又一个定理，即判定一个三角形是等边三角形的另外一种方法.

例1 如图，已知∠A=36°，∠DBC=36°，∠C=72°,计算∠1和∠2的度数，并说明图中有哪些等腰三角形.

解：∵∠A=36°∠DBC= 36° ∠C= 72°

∴∠2=180 °－ ∠A － ∠DBC － ∠C ＝ 36°

(三角形内角和定理）

∴ ∠A＝ ∠2

∴AD=BD(等角对等边）

∵ ∠1= ∠A ＋∠2= 72°= ∠C

∴BD=BC (等角对等边）

∴图中的等腰三角形有△ADB、△ABC、△BDC三个.

例2 如图，CD是等腰直角三角形ABC斜边上的高，找出图中有哪些等腰直角三角形。

答：图中的等腰直角三角形有：

等腰Rt△ABC、等腰Rt△ADC和等腰Rt△ CDB

用反证法证题的一般步骤

1. 假设命题的结论不成立;

2. 从这个假设出发,应用正确的推理方法, 得出与定义、基本事实、已有定理或已知条件 相矛盾的结果;

3. 由矛盾的结果判定假设不正确,从而肯定命题的结论正确.