《一元一次不等式与一次函数》一元一次不等式和一元一次不等式组PPT下载(第1课时)

北师大版八年级数学下册《一元一次不等式与一次函数》一元一次不等式和一元一次不等式组PPT下载(第1课时)，共16页。

讲授新课

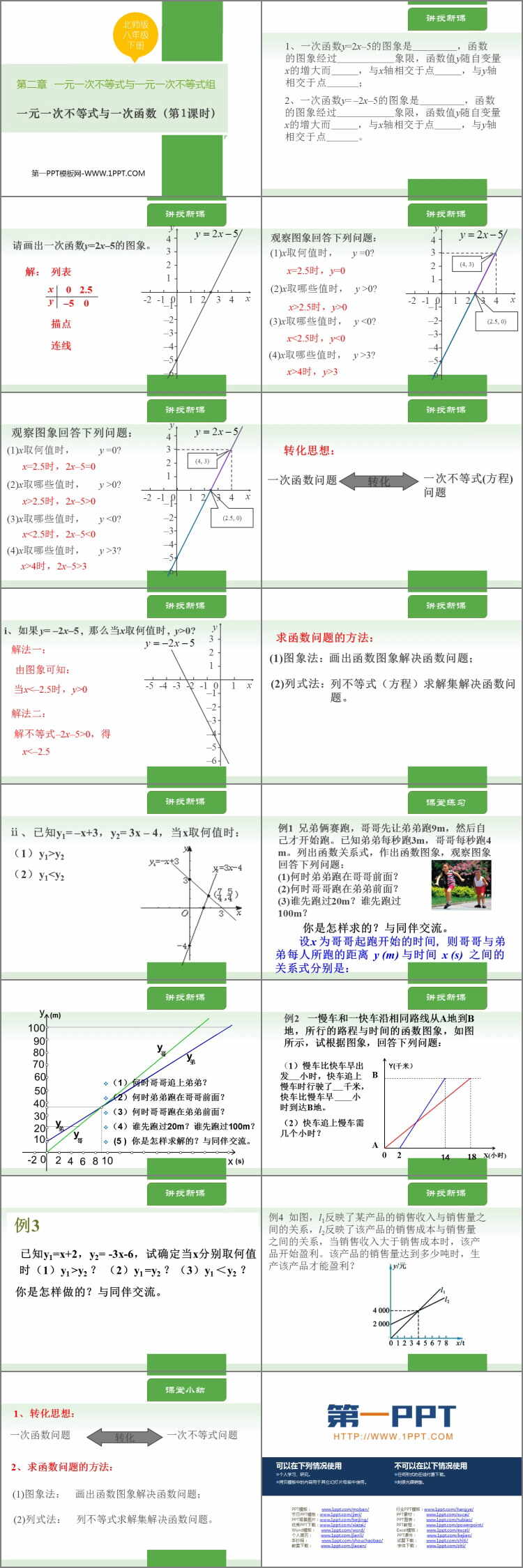
请画出一次函数y=2x–5的图象。

观察图象回答下列问题：

(1)x取何值时，y =0?

x=2.5时，y=0

(2)x取哪些值时，y >0?

x>2.5时，y>0

(3)x取哪些值时，y <0?

x<2.5时，y<0

(4)x取哪些值时，y >3?

x>4时，y>3

观察图象回答下列问题：

(1)x取何值时，y =0?

x=2.5时，2x–5=0

(2)x取哪些值时，y >0?

x>2.5时，2x–5>0

(3)x取哪些值时，y <0?

x<2.5时，2x–5<0

(4)x取哪些值时，y >3?

x>4时，2x–5>3

求函数问题的方法：

(1)图象法：画出函数图象解决函数问题；

(2)列式法：列不等式（方程）求解集解决函数问题。

课堂练习

例1 兄弟俩赛跑，哥哥先让弟弟跑9m，然后自己才开始跑。已知弟弟每秒跑3m，哥哥每秒跑4m。列出函数关系式，作出函数图象，观察图象

回答下列问题：

(1)何时弟弟跑在哥哥前面？

(2)何时哥哥跑在弟弟前面？

(3)谁先跑过20m？谁先跑过100m？

设x 为哥哥起跑开始的时间, 则哥哥与弟弟每人所跑的距离 y (m) 与时间 x (s) 之间的关系式分别是：

（1）何时哥哥追上弟弟？

（2）何时弟弟跑在哥哥前面？

（3）何时哥哥跑在弟弟前面？

（4）谁先跑过20m？谁先跑过100m？

（5 ) 你是怎样求解的？与同伴交流。

例2 一慢车和一快车沿相同路线从A地到B地，所行的路程与时间的函数图象，如图所示，试根据图象，回答下列问题：

（1）慢车比快车早出发 小时，快车追上慢车时行驶了____千米，快车比慢车早____小时到达B地。

（2）快车追上慢车需几个小时？

例3已知y1=x+2，y2= -3x-6，试确定当x分别取何值时（1）y1 >y2 ？ （2）y1 =y2 ？（3）y1 ＜y2 ？

你是怎样做的？与同伴交流。