《矩形的性质与判定》特殊平行四边形PPT教学课件(第3课时)

北师大版九年级数学上册《矩形的性质与判定》特殊平行四边形PPT教学课件(第3课时)，共23页。

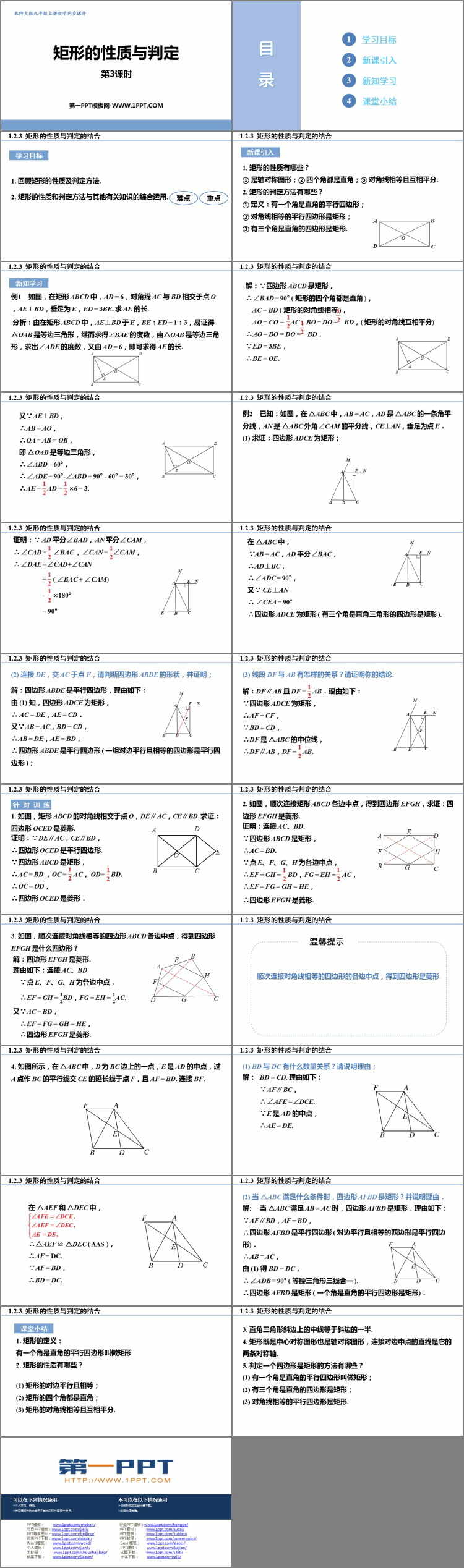
学习目标

1. 回顾矩形的性质及判定方法.

2. 矩形的性质和判定方法与其他有关知识的综合运用.

新课引入

1. 矩形的性质有哪些？

① 是轴对称图形；② 四个角都是直角；③ 对角线相等且互相平分.

2. 矩形的判定方法有哪些？

① 定义：有一个角是直角的平行四边形；

② 对角线相等的平行四边形是矩形；

③ 有三个角是直角的四边形是矩形.

新知学习

例1如图，在矩形 ABCD 中，AD = 6，对角线 AC 与 BD 相交于点 O ，AE⊥BD，垂足为 E，ED = 3BE. 求 AE 的长.

分析：由在矩形 ABCD 中，AE⊥BD 于 E，BE：ED = 1：3，易证得 △OAB 是等边三角形，继而求得∠BAE 的度数，由△OAB 是等边三角形，求出∠ADE 的度数，又由 AD = 6，即可求得 AE 的长.

例2已知：如图，在 △ABC 中，AB = AC，AD 是 △ABC 的一条角平分线，AN 是 △ABC 外角∠CAM 的平分线，CE⊥AN，垂足为点 E．

(1) 求证：四边形 ADCE 为矩形；

(2) 连接 DE，交 AC 于点 F，请判断四边形 ABDE 的形状，并证明；

(3) 线段 DF 与 AB 有怎样的关系？请证明你的结论.

针对训练

1. 如图，矩形 ABCD 的对角线相交于点 O，DE∥AC，CE∥BD. 求证：四边形 OCED 是菱形.

2. 如图，顺次连接矩形 ABCD 各边中点，得到四边形 EFGH，求证：四边形 EFGH 是菱形.

3. 如图，顺次连接对角线相等的四边形 ABCD 各边中点，得到四边形 EFGH 是什么四边形？

课堂小结

1. 矩形的定义：有一个角是直角的平行四边形叫做矩形

2. 矩形的性质有哪些？

(1) 矩形的对边平行且相等；

(2) 矩形的四个角都是直角；

(3) 矩形的对角线相等且互相平分.

3. 直角三角形斜边上的中线等于斜边的一半.

4. 矩形既是中心对称图形也是轴对称图形，连接对边中点的直线是它的两条对称轴.

5. 判定一个四边形是矩形的方法有哪些？

(1) 有一个角是直角的平行四边形叫做矩形；

(2) 有三个角是直角的四边形是矩形；

(3) 对角线相等的平行四边形是矩形.