《线段的垂直平分线》PPT教学课件(第2课时)

冀教版八年级数学上册《线段的垂直平分线》PPT教学课件(第2课时)，共19页。

学 习 目 标

理解并掌握线段垂直平分线的逆定理并学会运用.（重点）

能够运用线段垂直平分线的性质定理和逆定理解决实际问题.（难点）

知识讲解

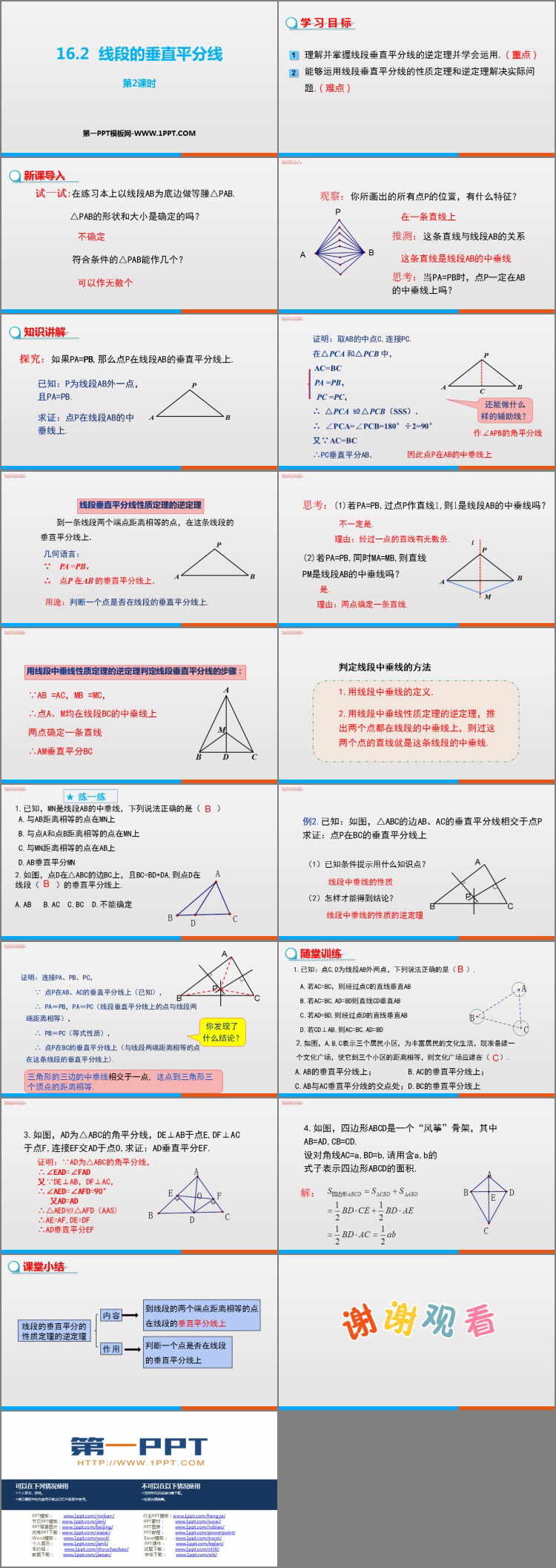
探究：如果PA=PB,那么点P在线段AB的垂直平分线上.

已知：P为线段AB外一点，且PA=PB.

求证：点P在线段AB的中垂线上.

证明：取AB的中点C,连接PC.

在△PCA 和△PCB 中，

AC=BC

PA =PB，

PC =PC，

∴△PCA ≌△PCB（SSS）．

∴∠PCA=∠PCB=180°÷2=90°

又∵AC=BC

∴PC垂直平分AB．

线段垂直平分线性质定理的逆定理

到一条线段两个端点距离相等的点，在这条线段的垂直平分线上．

几何语言：

∵PA =PB，

∴点P 在AB 的垂直平分线上．

用途：判断一个点是否在线段的垂直平分线上.

判定线段中垂线的方法

1.用线段中垂线的定义.

2.用线段中垂线性质定理的逆定理，推出两个点都在线段的中垂线上，则过这两个点的直线就是这条线段的中垂线.

例2.已知：如图，△ABC的边AB、AC的垂直平分线相交于点P求证：点P在BC的垂直平分线上

（1）已知条件提示用什么知识点？

线段中垂线的性质

（2）怎样才能得到结论？

线段中垂线的性质的逆定理

证明：连接PA、PB、PC，

∵ 点P在AB、AC的垂直平分线上（已知），

∴ PA＝PB，PA＝PC（线段垂直平分线上的点与线段两端距离相等），

∴ PB＝PC（等式性质），

∴ 点P在BC的垂直平分线上（与线段两端距离相等的点在这条线段的垂直平分线上).

三角形的三边的中垂线相交于一点，这点到三角形三个顶点的距离相等.